
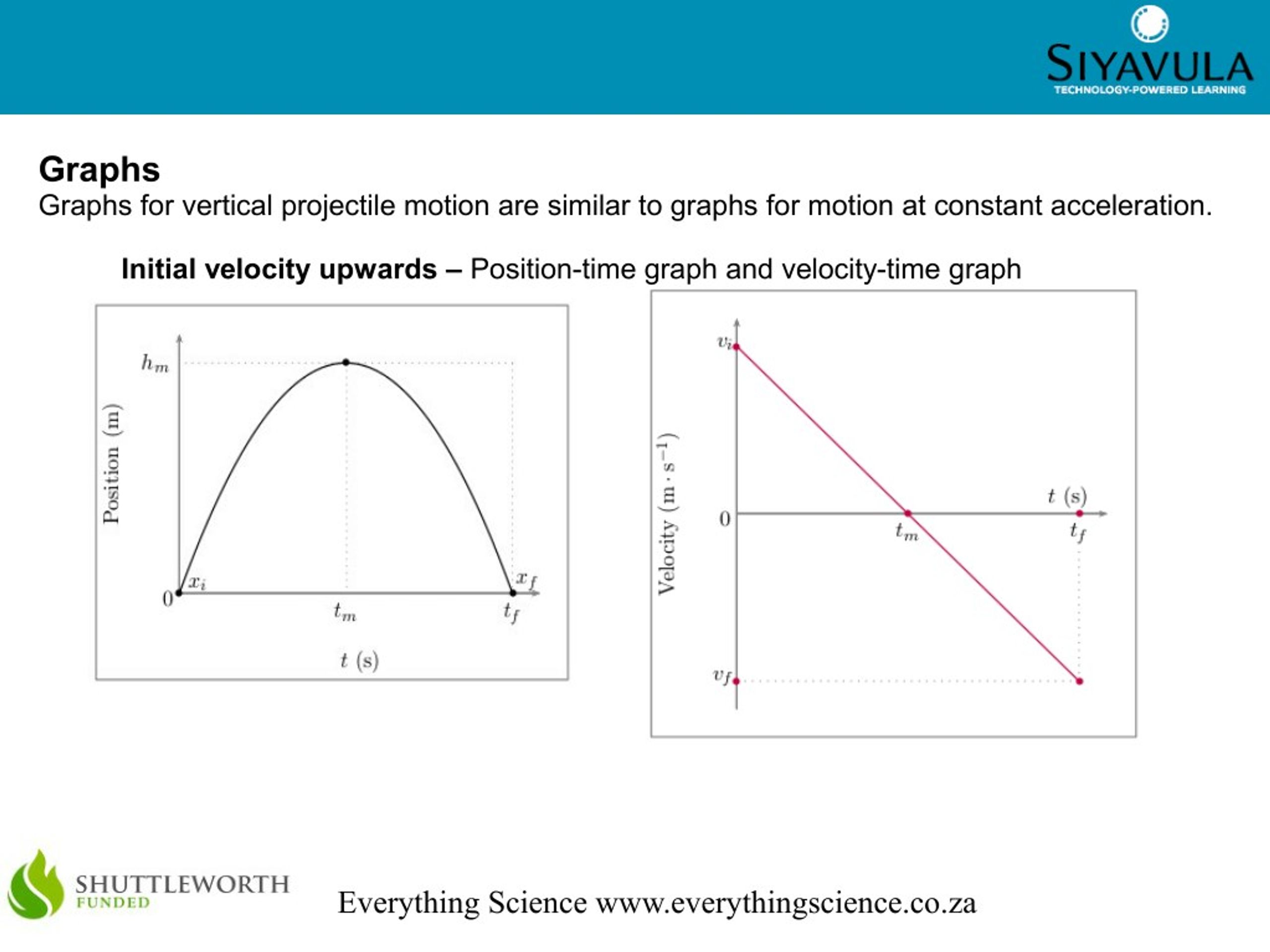
# calculate new angle for force separationĪ, v = np.array(), np.array(, vy])Īng = np.arccos( np.dot(a,v) / (1*np.linalg.norm(v)) )Īng = 2*np.pi - np.arccos( np.dot(a,v) / (1*np.linalg. Draw two velocity vs time graphs for the motions in horizontal direction and vertical direction. in the end of the flight the drag force in y direction has an opposite sign than gravity)ĭo for example: vel = np.sqrt(vx**2 + vy**2) Question: Below is a graph to show the projectile motion. This is because in every step you have new angle (i.e. The formula for 'the total time the projectile is in the air' is the formula for t. The angles range from 25 to 60 and each initial angle should have its own line on the graph. I am trying to graph a projectile through time at various angles. When calculating the new velocities you also have to compute an updated angle. projectile motion simple simulation using numpy matplotlib python. Also work with numpy arrays as vectors instead of having vx and vy separately.Īdditionally there is an error in your calculations.

Implement for example a function which calculates a new time step.
PROJECTILE MOTION GRAPH CODE
This makes your code easier to read and more reusable. Generally try to work with functions you can then call in for loops.Yes you definitely have to include all parameters of the projectile as the total distance traveled is very sensitive to that.Print("Range of projectile is m".format(x)) # With the new velocity calculate the drag force T.append(t+dt) # increment by dt and add to the list of time # Create the lists for acceleration components # parameters for the projectile motion without drag force The black dotted line is then called the envelope of all these lines, and is the boundary line formed when I plot quadratics for every possible angle between 0 and pi. In the graph above I have changed the launch angle to generate different quadratics. Vx = # list for velocity x and y components For any given launch angle and for a fixed initial velocity we will get projectile motion. # Start by putting the initial velocities at t=0 G = 9.8 # Acceleration due to gravity (m/s^2)Īng = 60.0 # Angle of initial velocity in degree It would be awesome if you're also willing to point out any errors I've made import numpy as np Is the way I'm doing it very complicated and how would you modify it to make it more efficient and neat? What caused this? Is it because the drag force I've put only includes drag coefficient and velocity, which made the graph smaller than the one that also has cross sectional area and rho included?


(the smaller one is the one with drag while the bigger one is the one without it) There's a big difference between this two lines in terms of the range as the other similar graphs I've come across online only show a slight difference. However, the resulted graph has come as a surprise for me as it looks a bit off. In order to make a comparison, I tried to plot a projectile motion without air resistance in the same graph with the same parameters on my own. It has guided me to do the projectile motion with air resistance. I started off by following this exercise. $t$ plot is (almost) identical to case 2.I'm simulating the projectile motions with python on Spyder, one with air resistance and one without it. It is described completely by the one-dimensional SUVAT equation $s_y(t) = u_y t + \fract$ The lower axis in time represents the rise and fall of the body in the vertical axis of displacement, making no statement about its horizontal motion. The vertical axis for a projectile motion graph is generally always vertical displacement/height/vertical position, etc.īoth a lower axis in time and a lower axis in horizontal displacement are valid choices.


 0 kommentar(er)
0 kommentar(er)
